深度优先搜索(使用Java实现)(赛前专项复习)

77.组合

77. 组合 - 力扣（LeetCode）

给定两个整数 n 和 k，返回范围 [1, n] 中所有可能的 k 个数的组合。
你可以按 任何顺序 返回答案。

示例 1：

输入： n = 4, k = 2
输出：
[
[2,4],
[3,4],
[2,3],
[1,2],
[1,3],
[1,4],
]

示例 2：

输入： n = 1, k = 1
输出：[[1]]

提示：

• 1 <= n <= 20
• 1 <= k <= n

class Solution {
    List<List<Integer>> result = new ArrayList<>();
    List<Integer> path = new ArrayList<>();
    void dfs(int start, int size, int n, int k){
        if(size==k){
            result.add(new ArrayList<>(path));
            return;
        }
        for(int i=start; i<=n; i++){
            path.addLast(i);
            dfs(i+1,size+1,n,k);
            path.remove(size);
        }
    }
    public List<List<Integer>> combine(int n, int k) {
        dfs(1,0,n,k);
        return result;
    }
}

注意, Java中Deque也是一种可迭代的集合, 那么new ArrayList<>()构造参数中只要是一种可迭代的集合即可, 那么对于回溯法来说, 最好是很方便尾插和尾删的集合, 那么有一种集合非常合适, 双端队列, Deque<Integer> path = new ArrayDeque<>();

不过在力扣中, 貌似使用ArrayList提交耗时更少, 会比Deque少2ms

下面对上面代码进行剪枝优化, 防止回溯到没有实际意义的分支

class Solution {
    List<List<Integer>> result = new ArrayList<>();
    List<Integer> path = new ArrayList<>();
    void dfs(int start, int size, int n, int k){
        if(size==k){
            result.add(new ArrayList<>(path));
            return;
        }
        for(int i=start; i<=n-(k-size)+1; i++){
            path.add(i);
            dfs(i+1,size+1,n,k);
            path.remove(size);
        }
    }
    public List<List<Integer>> combine(int n, int k) {
        dfs(1,0,n,k);
        return result;
    }
}

也就是说, 如果k=2,size=0,n=4, 那么再尝试数字4是没有意义的, 因为即使尝试完之后, 接着往下尝试一定会失败, 有意义的区间是从[start,n-(k-size)+1]闭区间

216. 组合总和 III

216. 组合总和 III - 力扣（LeetCode）

找出所有相加之和为 n 的 k 个数的组合，且满足下列条件：

• 只使用数字1到9
• 每个数字 最多使用一次

返回 所有可能的有效组合的列表 。该列表不能包含相同的组合两次，组合可以以任何顺序返回。

示例 1:

输入: k = 3, n = 7
输出: [[1,2,4]]
解释:
1 + 2 + 4 = 7
没有其他符合的组合了。

示例 2:

输入: k = 3, n = 9
输出: [[1,2,6], [1,3,5], [2,3,4]]
解释:
1 + 2 + 6 = 9
1 + 3 + 5 = 9
2 + 3 + 4 = 9
没有其他符合的组合了。

示例 3:

输入: k = 4, n = 1
输出: []
解释: 不存在有效的组合。
在[1,9]范围内使用4个不同的数字，我们可以得到的最小和是1+2+3+4 = 10，因为10 > 1，没有有效的组合。

提示:

• 2 <= k <= 9
• 1 <= n <= 60

class Solution {
    List<List<Integer>> res = new ArrayList<>();
    List<Integer> path = new ArrayList<>();
    void dfs(int start, int sum, int size, int k, int n){
        if(size==k){
            if(sum==n){
                res.add(new ArrayList<>(path));
            }
            return;
        }
        for(int i=start; i<10; i++){
            path.add(i);
            dfs(i+1,sum+i,size+1,k,n);
            path.remove(size);
        }
    }
    public List<List<Integer>> combinationSum3(int k, int n) {
        dfs(1,0,0,k,n);
        return res;
    }
}

剪枝有两个方面

1. size不能是的后面的操作没有意义, 也就是循环条件i<=9-(k-size)+1

2. sum不能超过n

39.组合总和

39. 组合总和 - 力扣（LeetCode）

给你一个 无重复元素 的整数数组 candidates 和一个目标整数 target ，找出 candidates 中可以使数字和为目标数 target 的 所有 不同组合 ，并以列表形式返回。你可以按 任意顺序 返回这些组合。

candidates 中的 同一个 数字可以 无限制重复被选取 。如果至少一个数字的被选数量不同，则两种组合是不同的。

对于给定的输入，保证和为 target 的不同组合数少于 150 个。

示例 1：

输入： candidates = [2,3,6,7], target = 7
输出：[[2,2,3],[7]]
解释：
2 和 3 可以形成一组候选，2 + 2 + 3 = 7 。注意 2 可以使用多次。
7 也是一个候选， 7 = 7 。
仅有这两种组合。

示例 2：

输入: candidates = [2,3,5],target = 8
输出: [[2,2,2,2],[2,3,3],[3,5]]

示例 3：

输入: candidates = [2], target = 1
输出: []

提示：

• 1 <= candidates.length <= 30
• 2 <= candidates[i] <= 40
• candidates 的所有元素 互不相同
• 1 <= target <= 40

本题的特殊点在于path中的元素可重复, 但是path是组合而不是排列, 不同顺序的排列看作同一种组合

所以本题首先需要candidates数组排好序, 且元素互不相同, 然后每次向下搜索的时候, 重复搜索一次之前的值, 而不是从i+1开始

class Solution {
    List<List<Integer>> res = new ArrayList<>();
    List<Integer> path = new ArrayList<>();
    void dfs(int[] candidates, int target, int size, int sum, int start){
        if(sum>target){
            return;
        }
        if(sum==target){
            res.add(new ArrayList<>(path));
            return;
        }
        for(int i=start; i<candidates.length; i++){
            path.add(candidates[i]);
            dfs(candidates,target,size+1,sum+candidates[i],i);
            path.remove(size);
        }
    }
    public List<List<Integer>> combinationSum(int[] candidates, int target) {
        dfs(candidates,target,0,0,0);
        return res;
    }
}

本题的剪枝操作, 除了最开始的sum>target, 还可以先对candidates进行排序, 随后在dfs()内的for循环中, 如果遇到了sum+candidates[i]>target, 就停止循环, 防止无意义重复递归

class Solution {
    List<List<Integer>> res = new ArrayList<>();
    List<Integer> path = new ArrayList<>();
    void dfs(int[] candidates, int target, int size, int sum, int start){
        if(sum>target){
            return;
        }
        if(sum==target){
            res.add(new ArrayList<>(path));
            return;
        }
        for(int i=start; i<candidates.length && sum+candidates[i]<=target; i++){
            path.add(candidates[i]);
            dfs(candidates,target,size+1,sum+candidates[i],i);
            path.remove(size);
        }
    }
    public List<List<Integer>> combinationSum(int[] candidates, int target) {
        Arrays.sort(candidates);
        dfs(candidates,target,0,0,0);
        return res;
    }
}

40.组合总和 II

给定一个候选人编号的集合 candidates 和一个目标数 target ，找出 candidates 中所有可以使数字和为 target 的组合。

candidates 中的每个数字在每个组合中只能使用 一次 。

注意： 解集不能包含重复的组合。

示例 1:

输入: candidates = [10,1,2,7,6,1,5], target = 8,
输出:
[
[1,1,6],
[1,2,5],
[1,7],
[2,6]
]

示例 2:

输入: candidates = [2,5,2,1,2], target = 5,
输出:
[
[1,2,2],
[5]
]

提示:

• 1 <= candidates.length <= 100
• 1 <= candidates[i] <= 50
• 1 <= target <= 30

本题的特殊点在于, candidates中元素有重复

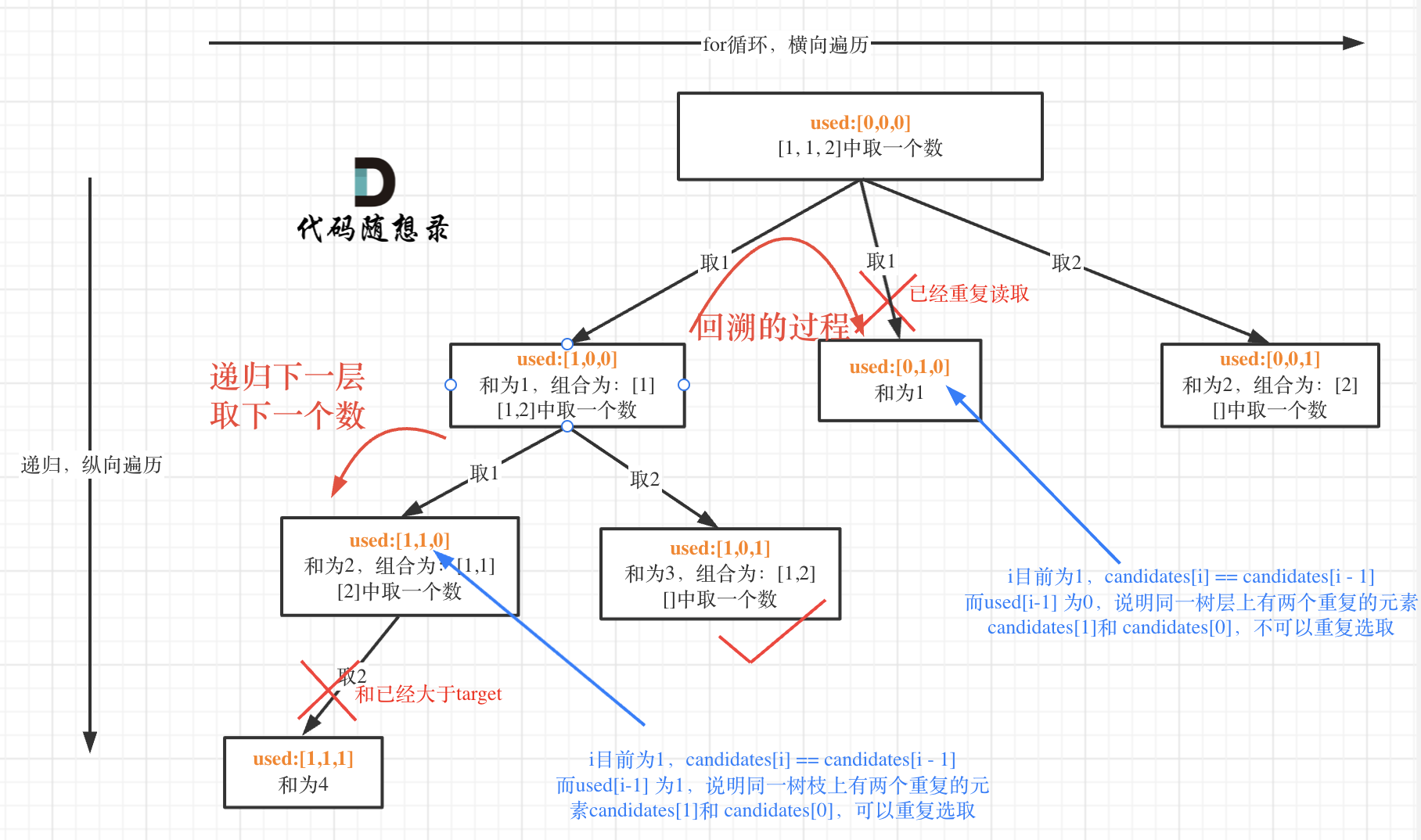
所以我们的目的只有一个, 那就是同一层不能选取重复的, 见下边

层	used	path
1	1,0,0	1
2	1,0,1	1,2
1	0,1,0	1
2	0,1,1	1,2

也就是说, 一旦同一层选择了重复的, 那么接着向下搜索的时候, 一定会造成重复, 但是同一根分支向下搜索可以重复

所以综合来看, 可以使用used来避免本层重复, 也可以使用hashSet来避免本层重复, 每一层新建一个hashSet, 本层遍历的时候, 每进入一次循环, 就将candidates[i]放入hashSet, 如果遇到, 重复的元素, 就能及时发现

所以不需要在res层面对path去重, 只需要在每一层防止遍历相同元素即可

使用set去重的版本相对于used数组的版本效率都要低很多

因为程序运行的时候对unordered_set 频繁的insert，unordered_set需要做哈希映射（也就是把key通过hash function映射为唯一的哈希值）相对费时间，而且insert的时候其底层的符号表也要做相应的扩充，也是费时的。

而使用used数组在时间复杂度上几乎没有额外负担！

如果使用set去重，空间复杂度就变成了O(n^2)，因为每一层递归都有一个set集合，系统栈空间是n(深度优先搜索有n层)，每一个空间都有set集合。

used数组只开辟过一次空间, 只需要O(n)

class Solution {
    List<List<Integer>> res = new ArrayList<>();
    List<Integer> path = new ArrayList<>();
    void dfs(int start, int size, int sum, boolean[] used, int[] candidates, int target){
        if(sum==target){
            res.add(new ArrayList<>(path));
            return;
        }
        for(int i=start; i<candidates.length && sum+candidates[i]<=target; i++){
            if(i>0 && !used[i-1] && candidates[i-1]==candidates[i]){
                continue;
            }
            used[i] = true;
            path.add(candidates[i]);
            dfs(i+1,size+1,sum+candidates[i],used,candidates,target);
            used[i] = false;
            path.remove(size);
        }
    }
    public List<List<Integer>> combinationSum2(int[] candidates, int target) {
        Arrays.sort(candidates);
        boolean[] used = new boolean[candidates.length];
        dfs(0,0,0,used,candidates,target);
        return res;
    }
}

78.子集

78. 子集 - 力扣（LeetCode）

给你一个整数数组 nums ，数组中的元素 互不相同 。返回该数组所有可能的子集（幂集）。

解集 不能 包含重复的子集。你可以按 任意顺序 返回解集。

示例 1：

输入： nums = [1,2,3]
输出：[[],[1],[2],[1,2],[3],[1,3],[2,3],[1,2,3]]

示例 2：

输入： nums = [0]
输出：[[],[0]]

提示：

• 1 <= nums.length <= 10
• -10 <= nums[i] <= 10
• nums 中的所有元素 互不相同

class Solution {
    List<List<Integer>> res = new ArrayList<>();
    List<Integer> path = new ArrayList<>();
    void dfs(int[] nums, int size, int start){
        res.add(new ArrayList<>(path));
        if(size==nums.length){
            return;
        }
        for(int i=start; i<nums.length; i++){
            path.add(nums[i]);
            dfs(nums,size+1,i+1);
            path.remove(size);
        }
    }
    public List<List<Integer>> subsets(int[] nums) {
        dfs(nums,0,0);
        return res;
    }
}

90.子集II

90. 子集 II - 力扣（LeetCode）

给你一个整数数组 nums ，其中可能包含重复元素，请你返回该数组所有可能的子集（幂集）。

解集 不能 包含重复的子集。返回的解集中，子集可以按 任意顺序 排列。

示例 1：

输入： nums = [1,2,2]
输出：[[],[1],[1,2],[1,2,2],[2],[2,2]]

示例 2：

输入： nums = [0]
输出：[[],[0]]

提示：

• 1 <= nums.length <= 10
• -10 <= nums[i] <= 10

class Solution {
    List<List<Integer>> res = new ArrayList<>();
    List<Integer> path = new ArrayList();
    void dfs(int[] nums, boolean[] used, int size, int start){
        res.add(new ArrayList<>(path));
        if(size==nums.length){
            return;
        }
        for(int i=start; i<nums.length; i++){
            if(i>0 && nums[i-1]==nums[i] && !used[i-1])
                continue;
            path.add(nums[i]);
            used[i] = true;
            dfs(nums,used,size+1,i+1);
            path.remove(size);
            used[i] = false;
        }
    }
    public List<List<Integer>> subsetsWithDup(int[] nums) {
        Arrays.sort(nums);
        boolean[] used = new boolean[nums.length];
        dfs(nums,used,0,0);
        return res;
    }
}

46.全排列

给定一个不含重复数字的数组 nums ，返回其 所有可能的全排列 。你可以 按任意顺序 返回答案。

示例 1：

输入： nums = [1,2,3]
输出：[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]

示例 2：

输入： nums = [0,1]
输出：[[0,1],[1,0]]

示例 3：

输入： nums = [1]
输出：[[1]]

提示：

• 1 <= nums.length <= 6
• -10 <= nums[i] <= 10
• nums 中的所有整数 互不相同

class Solution {
    List<List<Integer>> res = new ArrayList<>();
    List<Integer> path = new ArrayList<>();
    void dfs(int[] nums,boolean[] used, int size){
        if(size==nums.length){
            res.add(new ArrayList<>(path));
            return;
        }
        for(int i=0; i<nums.length; i++){
            if(used[i])
                continue;
            path.add(nums[i]);
            used[i] = true;
            dfs(nums,used,size+1);
            path.remove(size);
            used[i] = false;
        }
    }
    public List<List<Integer>> permute(int[] nums) {
        boolean[] used = new boolean[nums.length];
        dfs(nums,used,0);
        return res;
    }
}

47.全排列II

47. 全排列 II - 力扣（LeetCode）

给定一个可包含重复数字的序列 nums ，按任意顺序 返回所有不重复的全排列。

示例 1：

输入： nums = [1,1,2]
输出：
[[1,1,2],
[1,2,1],
[2,1,1]]

示例 2：

输入： nums = [1,2,3]
输出：[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]

提示：

• 1 <= nums.length <= 8
• -10 <= nums[i] <= 10

class Solution {
    List<List<Integer>> res = new ArrayList<>();
    List<Integer> path = new ArrayList<>();
    void dfs(int[] nums, boolean[] used, int size){
        if(size==nums.length){
            res.add(new ArrayList<>(path));
            return;
        }
        for(int i=0; i<nums.length; i++){
            if(used[i])
                continue;
            if(i>0 && nums[i-1]==nums[i] && !used[i-1])
                continue;
            path.add(nums[i]);
            used[i] = true;
            dfs(nums,used,size+1);
            used[i] = false;
            path.remove(size);
        }
    }
    public List<List<Integer>> permuteUnique(int[] nums) {
        Arrays.sort(nums);
        boolean[] used = new boolean[nums.length];
        dfs(nums,used,0);
        return res;
    }
}

491.非递减子序列

给你一个整数数组 nums ，找出并返回所有该数组中不同的递增子序列，递增子序列中 至少有两个元素 。你可以按 任意顺序 返回答案。

数组中可能含有重复元素，如出现两个整数相等，也可以视作递增序列的一种特殊情况。

示例 1：

输入： nums = [4,6,7,7]
输出：[[4,6],[4,6,7],[4,6,7,7],[4,7],[4,7,7],[6,7],[6,7,7],[7,7]]

示例 2：

输入： nums = [4,4,3,2,1]
输出：[[4,4]]

提示：

• 1 <= nums.length <= 15
• -100 <= nums[i] <= 100

这道题需要在同一层中去重

如果使用used去重的话, 需要对nums排序, 但是本题不允许更改nums, 所以只能使用set去重

class Solution {
    List<List<Integer>> res = new ArrayList<>();
    List<Integer> path = new ArrayList<>();
    void dfs(int[] nums, int size, int start){
        if(size>1){
            res.add(new ArrayList<>(path));
        }
        HashSet<Integer> set = new HashSet<>();
        for(int i=start; i<nums.length; i++){
            if(set.contains(nums[i]))
                continue;
            if(size>0 && nums[i]<path.get(size-1))
                continue;
            set.add(nums[i]);
            path.add(nums[i]);
            dfs(nums,size+1,i+1);
            path.remove(size);
        }
    }
    public List<List<Integer>> findSubsequences(int[] nums) {
        dfs(nums,0,0);
        return res;
    }
}

797.所有可能的路径

797. 所有可能的路径 - 力扣（LeetCode）

给你一个有 n 个节点的 有向无环图（DAG），请你找出所有从节点 0 到节点 n-1 的路径并输出（不要求按特定顺序）

graph[i] 是一个从节点 i 可以访问的所有节点的列表（即从节点 i 到节点 graph[i][j]存在一条有向边）。

示例 1：

输入： graph = [[1,2],[3],[3],[]]
输出：[[0,1,3],[0,2,3]]
解释： 有两条路径 0 -> 1 -> 3 和 0 -> 2 -> 3

示例 2：

输入： graph = [[4,3,1],[3,2,4],[3],[4],[]]
输出：[[0,4],[0,3,4],[0,1,3,4],[0,1,2,3,4],[0,1,4]]

提示：

• n == graph.length
• 2 <= n <= 15
• 0 <= graph[i][j] < n
• graph[i][j] != i（即不存在自环）
• graph[i] 中的所有元素 互不相同
• 保证输入为 有向无环图（DAG）

class Solution {
    List<List<Integer>> res = new ArrayList<>();
    List<Integer> path = new ArrayList<>();
    void dfs(int[][] graph, int size, int end, int p){
        if(p==end){
            res.add(new ArrayList<>(path));
            return;
        }
        for(int i=0; i<graph[p].length; i++){
            path.add(graph[p][i]);
            dfs(graph,size+1,end,graph[p][i]);
            path.remove(size);
        }
    }
    public List<List<Integer>> allPathsSourceTarget(int[][] graph) {
        path.add(0);
        int end = graph.length-1;
        dfs(graph,1,end,0);
        return res;
    }
}