链表(使用C++实现)

😲创建结点示例

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
// 单链表节点
struct ListNode {
    int val;  // 节点上存储的元素
    ListNode *next;  // 指向下一个节点的指针
    ListNode(int x) : val(x), next(NULL) {}  // 节点的构造函数
};
int main(){
    // 使用自定义构造函数初始化, 创建指针变量并开辟实体内存空间
    ListNode* head = new ListNode(5);
    // 使用C++提供的默认构造函数, 然后通过赋值初始化
    ListNode* head = new ListNode();
    head->val = 5;

    return 0;
}

🤔一些疑问解答

链表在插入删除之前必须找到需要插入删除的位置, 那么为什么时间复杂度不是O(n)而是O(1)

这个时间复杂度说的是找到之后的删除和插入操作, 而不包含找到这个位置所消耗的时间
线性表删除需要讲后面的数据往前移动一格, 插入需要后面的数据往后移动一格, 所以是O(n)
链表只需要将指针存储的内存位置信息改动一下即可, 没有移动操作所以是O(1)

C++如何手动释放内存

Java、Python，就有自己的内存回收机制, C++最好自己手动释放内存
delete释放单个指针, delete[]释放指针数组

1
2
3
int* ptr = new int; // 动态分配一个int类型的对象
// 使用ptr
delete ptr; // 释放内存

如果使用new[]操作符动态分配了一个数组的内存，那么应该使用delete[]操作符来释放该内存。例如：

1
2
3
int* arr = new int[5]; // 动态分配一个包含5个int类型元素的数组
// 使用arr
delete[] arr; // 释放内存

💪力扣刷题

203. 移除链表元素

力扣传送门

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode() : val(0), next(nullptr) {}
 *     ListNode(int x) : val(x), next(nullptr) {}
 *     ListNode(int x, ListNode *next) : val(x), next(next) {}
 * };
 */
class Solution {
public:
    ListNode* removeElements(ListNode* head, int val) {
        // 创建一个虚拟头节点, 防止后面分类讨论第一个节点究竟等不等于val
        ListNode* pre = new ListNode(0);
        pre->next = head;
        // 创建一个用于遍历的指针
        ListNode* temp = pre;
        while(temp->next!=nullptr){
            // 定位到val节点的前一个, 然后删除它, 同时删除内存
            if(temp->next->val==val){
                ListNode* d = temp->next;
                temp->next = temp->next->next;
                delete d;
            }
            // 删除完成不要后移指针, 下一轮再判断一次, 如果temp->next->val!=val再考虑后移, 否则可能漏掉节点没判断
            else{
                temp = temp->next;
            }
        }
        return pre->next;
    }
};

206. 反转链表

力扣传送门

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode() : val(0), next(nullptr) {}
 *     ListNode(int x) : val(x), next(nullptr) {}
 *     ListNode(int x, ListNode *next) : val(x), next(next) {}
 * };
 */
class Solution {
public:
    ListNode* reverseList(ListNode* head) {
        ListNode* pre = nullptr;
        ListNode* tmp = head;
        while(tmp!=nullptr){
            ListNode* post = tmp->next;
            tmp->next = pre;
            pre = tmp;
            tmp = post;
        }
        return pre;
    }
};

24. 两两交换链表中的节点

力扣传送门

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode() : val(0), next(nullptr) {}
 *     ListNode(int x) : val(x), next(nullptr) {}
 *     ListNode(int x, ListNode *next) : val(x), next(next) {}
 * };
 */
class Solution {
public:
    ListNode* swapPairs(ListNode* head) {
        // 创建一个虚拟头指针
        ListNode* dummyhead = new ListNode(0,head);
        ListNode* tmp = dummyhead;
        ListNode* tmp2;
        ListNode* tmp3;
        while(tmp!=nullptr && tmp->next!=nullptr && tmp->next->next!=nullptr){
            // 记录两个位置
            tmp2 = tmp->next;
            tmp3 = tmp2->next->next;
            // 核心的三个操作
            tmp->next = tmp->next->next;
            tmp->next->next = tmp2;
            tmp2->next = tmp3;
            // tmp向后移动
            tmp = tmp2;
        }
        return dummyhead->next;
    }
};

指针变量本身所占的内存空间会在其作用域结束时自动释放，无需手动删除, 如tmp,tmp2,tmp3

实际上tmp不可能是空指针, 它只在后两个明确不是空指针的时候才进入循环, 每一轮循环结束的时候定位在后面第二个, 所以其实tmp不可能是空指针

tmp->next==nullptr和tmp->next->next==nullptr的情况不用判断, 都只需要直接返回即可, 因为tmp后面只剩一个或者一个不剩都不需要操作, 直接返回即可

19. 删除链表的倒数第 N 个结点

力扣传送门

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode() : val(0), next(nullptr) {}
 *     ListNode(int x) : val(x), next(nullptr) {}
 *     ListNode(int x, ListNode *next) : val(x), next(next) {}
 * };
 */
class Solution {
public:
    ListNode* removeNthFromEnd(ListNode* head, int n) {
        // 虚拟头节点, 避免分类讨论
        ListNode* dummyhead = new ListNode(0,head);
        // 双指针
        ListNode* tmp1 = dummyhead;
        ListNode* tmp2 = tmp1;
        // 让两个指针中间间隙大小为n
        while(n-->0){
            tmp2 = tmp2->next;
        }
        // 同时向后移动, 知道后一个指针移动到最后一个
        while(tmp2->next!=nullptr){
            tmp1 = tmp1->next;
            tmp2 = tmp2->next;
        }
        // 前一个指针的位置进行删除操作
        ListNode* d = tmp1->next;
        tmp1->next = tmp1->next->next;
        delete d;
        return dummyhead->next;
    }
};

面试题 02.07. 链表相交

力扣传送门

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode(int x) : val(x), next(NULL) {}
 * };
 */
class Solution {
public:
    ListNode *getIntersectionNode(ListNode *headA, ListNode *headB) {
        // 定义两个指针用于指向长链表和短链表, 暂且认为A长B短, 统计完长度如若不对再交换地址
        ListNode* longOne = headA;
        ListNode* shortOne = headB;
        // 统计两个链表长度
        int longLen=0, shortLen=0;
        ListNode* tmp = headA;
        while(tmp!=NULL){
            longLen++;
            tmp = tmp->next;
        }
        tmp = headB;
        while(tmp!=NULL){
            shortLen++;
            tmp = tmp->next;
        }
        // 如果A短B长就交换指针
        if(longLen<shortLen){
            swap(longLen,shortLen);
            swap(longOne,shortOne);
        }
        // 让长链表上的指针往后移动, 让两个链表指针位于同一起点
        int move = longLen-shortLen;
        while(move-->0)
            longOne = longOne->next;
        // 定义返回值, 如果没找到符合要求的节点就返回NULL
        ListNode* rs = NULL;
        // 两个指针同步向后移动, 如果找到符合要求的节点就break
        while(longOne!=NULL){
            if(longOne==shortOne){
                rs = longOne;
                break;
            }
            longOne = longOne->next;
            shortOne = shortOne->next;
        }
        return rs;
    }
};

142. 环形链表 II

力扣传送门

统计链表大小肯定是不行的, 永远走不到头
如果想存下来所有节点的地址, 然后看看什么时候存到一个重复的地址, 这种方法固然逻辑上讲的通, 但是实际业务中的节点非常多, 那么这种方法必然十分占用空间, 也不行
可以用快慢指针, 快指针一次走两格, 慢指针一次走一格, 这样的话, 只要有圈, 那么快指针一定能从后面再绕一圈追上慢指针

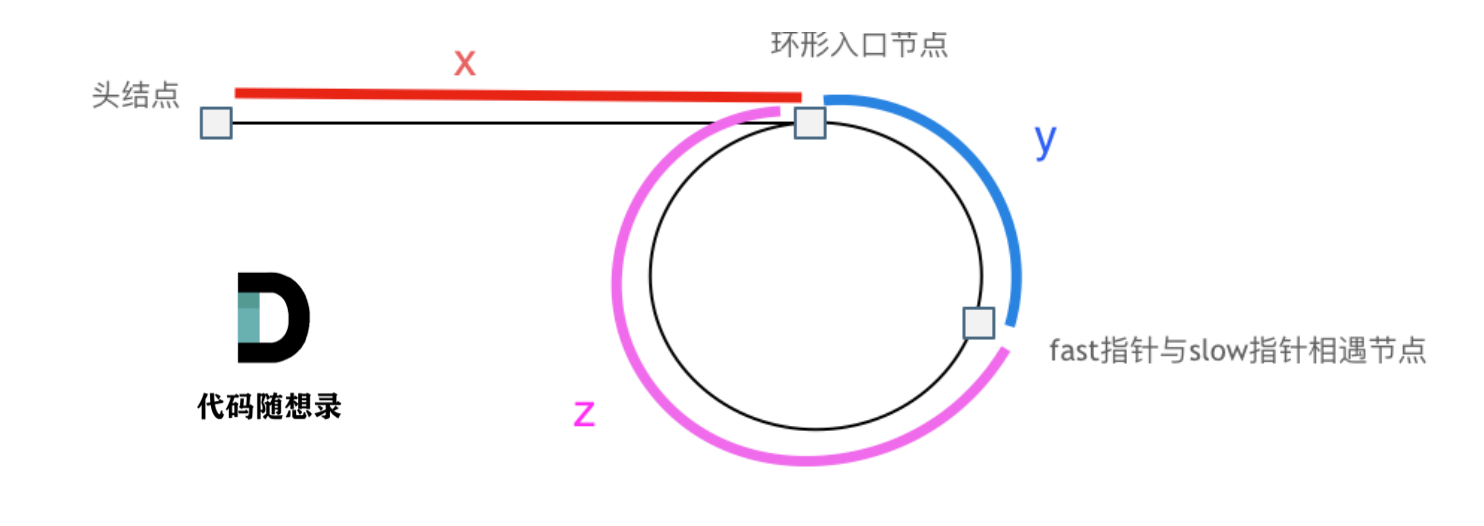
假设从头结点到环形入口节点 的节点数为x, 环形入口节点到 fast指针与slow指针相遇节点 节点数为y, 从相遇节点 再到环形入口节点节点数为 z

那么相遇时： slow指针走过的节点数为: x + y， fast指针走过的节点数：x + y + n (y + z)，n为fast指针在环内走了n圈才遇到slow指针， (y+z)为 一圈内节点的个数A。

因为fast指针是一步走两个节点，slow指针一步走一个节点， 所以 fast指针走过的节点数 = slow指针走过的节点数 * 2：

(x + y) * 2 = x + y + n (y + z)

两边消掉一个(x+y): x + y = n (y + z)

因为要找环形的入口，那么要求的是x，因为x表示 头结点到 环形入口节点的的距离。

所以要求x ，将x单独放在左面：x = n (y + z) - y ,

再从n(y+z)中提出一个 (y+z)来，整理公式之后为如下公式：x = (n - 1) (y + z) + z 注意这里n一定是大于等于1的，因为 fast指针至少要多走一圈才能相遇slow指针

这个公式说明什么呢？

先拿n为1的情况来举例，意味着fast指针在环形里转了一圈之后，就遇到了 slow指针了

当 n为1的时候，公式就化解为 x = z，

这就意味着，从头结点出发一个指针，从相遇节点也出发一个指针，这两个指针每次只走一个节点， 那么当这两个指针相遇的时候就是 环形入口的节点

如果n不等于1, 情况也一样, 仍然会相遇, 只不过从相遇节点出发的指针需要走几圈才能碰上另一个指针

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode(int x) : val(x), next(NULL) {}
 * };
 */
class Solution {
public:
    ListNode *detectCycle(ListNode *head) {
        ListNode* fast = head;
        ListNode* slow = head;
        while(fast!=NULL && fast->next!=NULL){
            slow = slow->next;
            fast = fast->next->next;
            if(fast==slow)
                break;
        }
        if(fast==NULL || fast->next==NULL)
            return NULL;
        ListNode* find = head;
        while(fast!=find){
            fast = fast->next;
            find = find->next;
        }
        return find;
    }
};
技术笔记
#算法 #数据结构 #C++ #力扣刷题 #Java转C++
链表(使用C++实现)
http://example.com/链表/
作者
李小基
许可协议